Точность результата измерений (точность измерений) – одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Поскольку точность измерения тем выше, чем меньше его погрешность, для количественной характеристики точности измерений обычно используют значения погрешностей.

Погрешность результата измерения (погрешность измерения) – отклонение результата измерения от истинного (действительного) значения измеряемой величины.

Упоминание в определении действительного значения измеряемой величины некорректно, поскольку само оно не совпадает с истинным значением измеряемой величины, и, следовательно, не может быть базой для отсчета погрешности. Погрешность измерения можно представить в виде разности между результатом измерения (полученным при измерении значением физической величины) и истинным значением физической величины

∆ = х – Q,

где ∆ – погрешность измерения,

х – результат измерения (полученное при измерении значение физической величины),

Q – истинное значение физической величины.

Измерения необходимы для оценки любого объекта трансформации (сырья, заготовки, детали, сборочной единицы) до ее начала, во время ее проведения и по окончании. В любом технологическом процессе надо знать, с чем приходится работать, чтобы планировать сам процесс, следить за тем как процесс идет, чтобы при необходимости корректировать его. Результат переработки исходного объекта тоже подлежит измерениям для оценки его качества и принятия управляющих решений (пропустить далее в обработку, продажу, эксплуатацию, забраковать, вернуть на переработку, корректировать техпроцесс...).

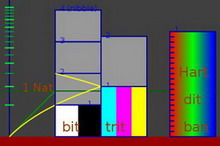
Определяющее значение измерения имеют и для любых экспериментальных исследований. Д.И.Менделеев сказал: «Наука начинается там, где начинают измерять. Точная наука немыслима без меры». Галилео Галилею приписывают слова: «Измерять то, что измеримо, делать измеримым то, что пока что неизмеримо». Место измерений в экспериментальных научных исследованиях, проводимых с использованием не только визуальных, но и аппаратурных средств фиксации результатов, показано на рисунке 1.5.

Достоверные результаты исследований и выводы из них могут быть получены только при «опережающей точности измерений». Любой тонкий эффект можно зафиксировать только тогда, когда измерения позволяют выделить его из информационного шума, в том числе и обусловленного погрешностями измерений.

Обмен результатами производственной и научной деятельности, международная кооперация в науке, промышленности и торговле требуют обеспечения достоверности всех результатов производственных и научных измерений. Поэтому в метрологии вводятся такие понятия, какединство измерений и единообразие средств измерений.

Единство измерений – состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.

Обеспечение единства измерений необходимо для обеспечения современного производства с разделением труда и кооперацией как в масштабах одной страны, так и в международных промышленно-экономических отношениях. Вот почему с давних пор активно работают международные метрологические организации, принимаются общие для всех метрологические стандарты, гармонизируются требования к измерениям, к средствам измерений, к оценке их метрологических характеристик.

Под единообразием средств измерений понимают состояние средств измерений, характеризующееся тем, что они проградуированы в узаконенных единицах и их метрологические свойства соответствуют нормам. Для обеспечения единообразия приходится разрабатывать представления об эталонах единиц физических величин, создавать эталоны как технические устройства, передавать значение единицы от эталонов другим, менее точным средствам измерений. Единообразие средств измерений есть необходимое, но недостаточное условие соблюдения единства измерений.

Метрология использует для повышения точности измерений новейшие достижения физики и других наук. Постоянно создаются новые, все более точные средства измерений, включая эталоны, совершенствуются методы измерений и передачи единиц физических величин рабочим средствам измерений, а также методы выявления и оценки погрешностей измерений. В соответствии с требованиями обеспечения единства измерений метрология уделяет особое внимание поиску и исключению систематических погрешностей измерений, а также вероятностной оценке случайных погрешностей, которые невозможно прогнозировать и оценивать другими методами.

Особое место в метрологии занимает математическая обработка результатов измерений. Для обработки результатов косвенных измерений, для построения моделей объектов измерений и процессов измерительного преобразования, для оценки систематических погрешностей используют различные разделы математического анализа, аналитической геометрии и других областей «детерминированной» математики. Наряду с этим широко используется аппарат теории вероятностей и математической статистики для оценки случайных составляющих погрешности измерений.

На сегодняшний день можно признать существование объективно сложившихся теоретических основ в следующих областях измерений:

- физические измерения в макромире (включая технические измерения);

- квантово-механические измерения;

- психологические измерения;

- кибернетические измерения;

- математические измерения.

Есть и другие пока еще недостаточно четко оформившиеся области измерений.

Физическими измерениями занимается метрология, одним из приоритетов которой является «теория погрешностей измерения».

Квантовомеханические измерения фактически основаны на взаимодействии микрообъекта с измерительным макроприбором.

Психологические и им подобные измерения (измерения в социологии, психологии, системотехнике и других подобных областях) сводятся к выбору типа шкалы и «помещению» объекта в некоторую ее область.

В кибернетических измерениях в первую очередь рассматривают воздействие помех в измерительном канале на искажение измерительной информации. Специально для этих целей разработана «информационная теория измерений».

Математические измерения (например, в геометрии) основаны на допущении «идеальных измерений», результаты которых свободны от погрешностей. Но изучение измерения как некоторого способа (алгоритма) получения числового результата в ходе измерительного эксперимента привело к разработке «алгоритмической теории измерения», где основное внимание уделяют измерению как процессу, который должен быть выполнен в соответствии с рационально построенным алгоритмом.

«Частные теории измерений» необходимы для использования в конкретных областях, а метрология как общенаучная область акцентирует внимание на следующих проблемах:

- Создание единиц и систем единиц, необходимых для реализации измерений.

- Методы выявления и оценивания погрешностей измерений.

- Математическая обработка и представление результатов измерений.