E (число)

e (число)

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значение:

e = 2,718 281 828 459 045 235 360 287 471 352 662 497 757… (последовательность A001113 в OEIS)

Число e играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

Способы определения

Число e может быть определено несколькими способами.

Через предел:

(второй замечательный предел).

Как сумма ряда:

или .

Как единственное число a, для которого выполняется

Как единственное положительное число a, для которого верно

Свойства

Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция , где c — произвольная константа.

Число e иррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.

, см. формула Эйлера, в частности

Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»

Для любого комплексного числа z верны следующие равенства:

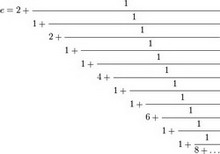
Число e разлагается в бесконечную цепную дробь следующим образом:

то есть

Представление Каталана:

История

Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен .

Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует.

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:

Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.

Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.

Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler).